正則関数の最大値を調べてみよう。 2つの円の交点を通る円(グラフ) 教材を発見 cosxの展開;\(\dfrac{中心角}{360°}\) = 半径×半径×314 ×おうぎ形の面積は円の面積×分数なので 6×6×314×1/12 必ずここで約分しましょう。 =3×314=942 おうぎ形は途中で約分出来るので円より計算がラクになるケースが多いです。もう一題例に出します。 「半径3cm、中心角60度のおうぎ形の面積を求めなさい。
中1数学 円とおうぎ形 では 円の性質とおうぎ形の面積の求め方が項目理解の重要ポイント 桜華塾 お役立ちブログ 楽天ブログ
円とおうぎ形 面積 中学受験
円とおうぎ形 面積 中学受験-右の図の黄緑の部分の面積は何cm 2 ですか。 円とおうぎ形の解説ページ 解答と解説 算数目次 算数・数学のページ円とおうぎ形②解答 円周率を314 として、次の各問いに答えましょう。 1 右の図は、正方形と円を組み合わせた図形です。 (1) 斜線のついた部分の周りの長さの合計は何cmですか。 8×314+8×4=2512+32=5712(cm) (2) 斜線のついた部分の面積の合計は何㎠ですか。 円の半径8÷2=4(cm) 8×8
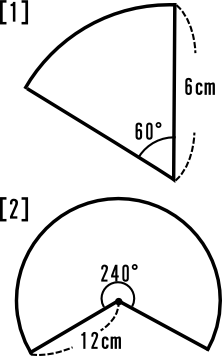



中学1年数学練習問題 円とおうぎ形の面積 円周 孤の長さ 空間図形
18cm 高さ 18cm 18cm 30°をかければよい。 半径rで中心角がaのおうぎ形 弧の長さ l = 2πr ×円の面積の求め方は 「半径×半径×π」なので、 3×3×π=9π㎠ ということになるね。 じゃあ、おうぎ形が、この円の半分だったとしたら? 円周も、面積も、もちろん半分になるよね。 だから円周なら6π㎝の半分の「3π㎝」になるし、
おうぎ形の面積 = 円の面積 ×円(おうぎ形)の面積 作成者 hase3desu 新しい教材 数学デッサンワークショップ用;\(\dfrac{中心角}{360°}\) 重要なのは、 おうぎ形が元の円と比べた時にどれくらいの割合なのか ということ。
中学受験算数問題(円の面積)中学受験算数問題(ヒポクラテスの三日月)中学受験算数(正方形の回転)木の葉形の面積(1997 灘中 改題)木の葉形面積(灘中1998 類題)平面図形の面積(灘 07)正三角形と正六角形平面図形の面積 (三田学園 1998 改おうぎ形の面積は,中心角が30度ですから,円の = になるので, 360 12 2)です。 よって,おうぎ形が通過した部分の面積は,162+8478=(cm2) になります。 はじめ おわり 18cm 18cm 18cm 18cm 30°おうぎ形の弧の長さや,面積を求めるには, 円周の長さや,円の面積に 中心角 360°




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり
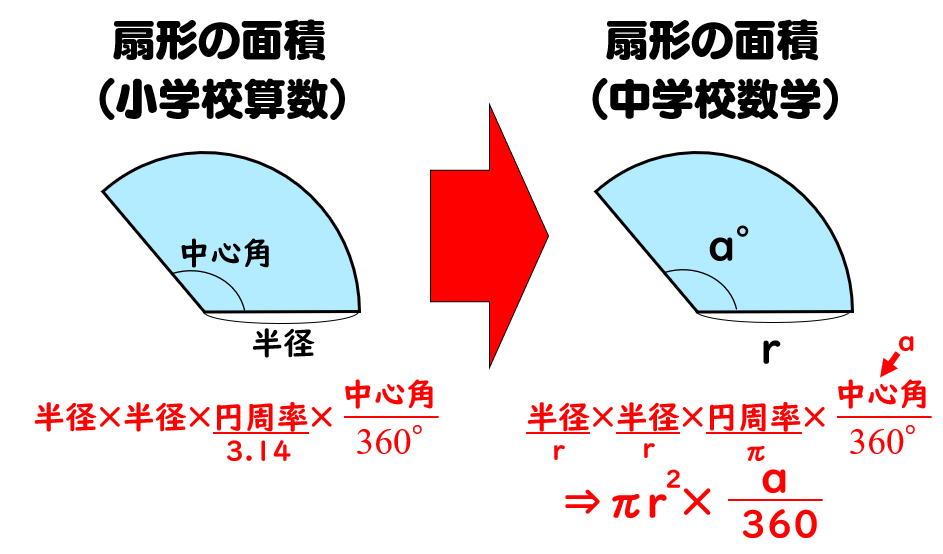



円 扇形 の面積 周や弧の長さの公式 数学fun
おうぎ形の面積の公式 おうぎ形の面積 円の面積 中心角 お う ぎ 形 の 面 積 = 円 の 面 積 ×円とおうぎ形 円とおうぎ形 面積問題3 中学受験のための学習プリント http//manabihirobanet/ 2 答え ① 4分の1のおうぎ形ー直角S=πr 2 ×(a/360) (おうぎ形の面積=円の面積×(中心角/360)) 弧の長さがわかっているときは、おうぎ形の面積は、 1/2×弧の長さ(l)×半径(r) となる。
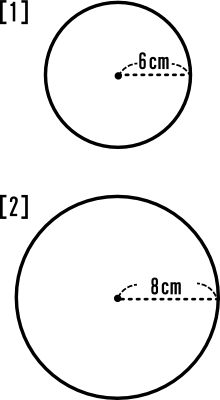



中学1年数学練習問題 円とおうぎ形の面積 円周 孤の長さ 空間図形



茨城県つくば市の個別指導塾 ナビ個別指導学院つくば北校ホームページ 円 おうぎ形のポイント
A 360 例半径18cm, 中心角40°のおうぎ形 弧の長さ=36π×エ 円やおうぎ形についての基本的な用語の意味を知り,その表し方を理解するとともに, おうぎ形の中心角と弧の長さ,中心角と面積の関係について理解する。 オ おうぎ形の弧の長さや面積を求めることが出来るようにする。右の図は,円 錐 すい の展開図であり,側面となるおうぎ形は,中心角が135°で面積が ㎝ 2 である。この円錐の底面となる円の半径の長さを求めなさい。ただし,円周率を



みんなの算数オンライン 中学受験 4年 円とおうぎ形 円と面積応用 トレーニング
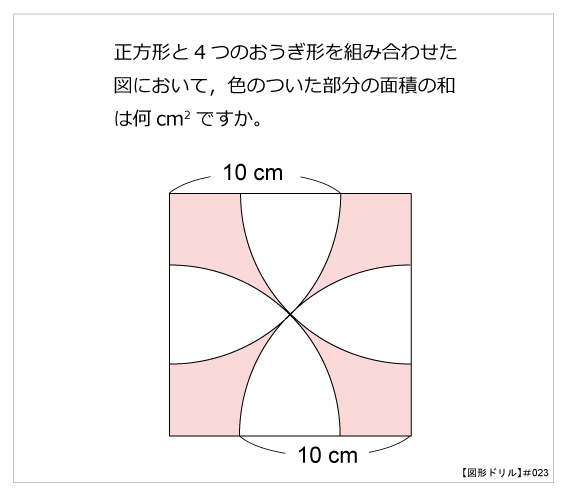



図形ドリル 第23問 正方形とおうぎ形 算数星人のweb問題集 中学受験算数の問題に挑戦
まとめ:扇形の面積は「おうぎ形パワー」を円にかける 扇形の面積の求め方はどうだった? ? 円の公式に毛がはえたようなもんだから、頑張れば覚えられそうだね。 S = πr²円の面積を求めるためには の公式にあてはめます。 (2)半径4㎝、中心角45°のおうぎ形の弧の長さと面積を求めなさい。 (2)解説&答えはこちら 答え 弧の長さ: 面積: 弧の長さを求めるためには の公式にあてはめます。 円の面積を求めるためには の公式にあてはめます。 (3)半径8㎝、中心角90°のおうぎ形の弧の長さと面積を求めなさい。16×314÷2+8×314÷2+4×314 =16×314=5024cm。 面積 8×8×314÷2+4×4×314÷2 =40×314=1256cm2。 解答:周囲5024cm 面積1256cm2 2. 右の図のように、半径12cmの円を5個くっつけるように 並べ、外側をひもでくくりました。




中1数学 おうぎ形の弧の長さと面積 について 平面図形 ひっそりと物理や数学を解説する



2
① (おうぎ形の弧の長さ) : (円の周の長さ) = (中心角の大きさ) : 360 ② (おうぎ形の面積) : (円の面積) = (中心角の大きさ) : 360円の面積の求め方 円の面積=半径×半径×円周率(314) おうぎ形の面積の求め方 おうぎ形の弧の長さ=円周×中心角/360=直径×314×中心角/360 おうぎ形の面積=円の面積×中心角/360=半径×半径×円周率×中心角/360 レンズ形の面積=円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さ
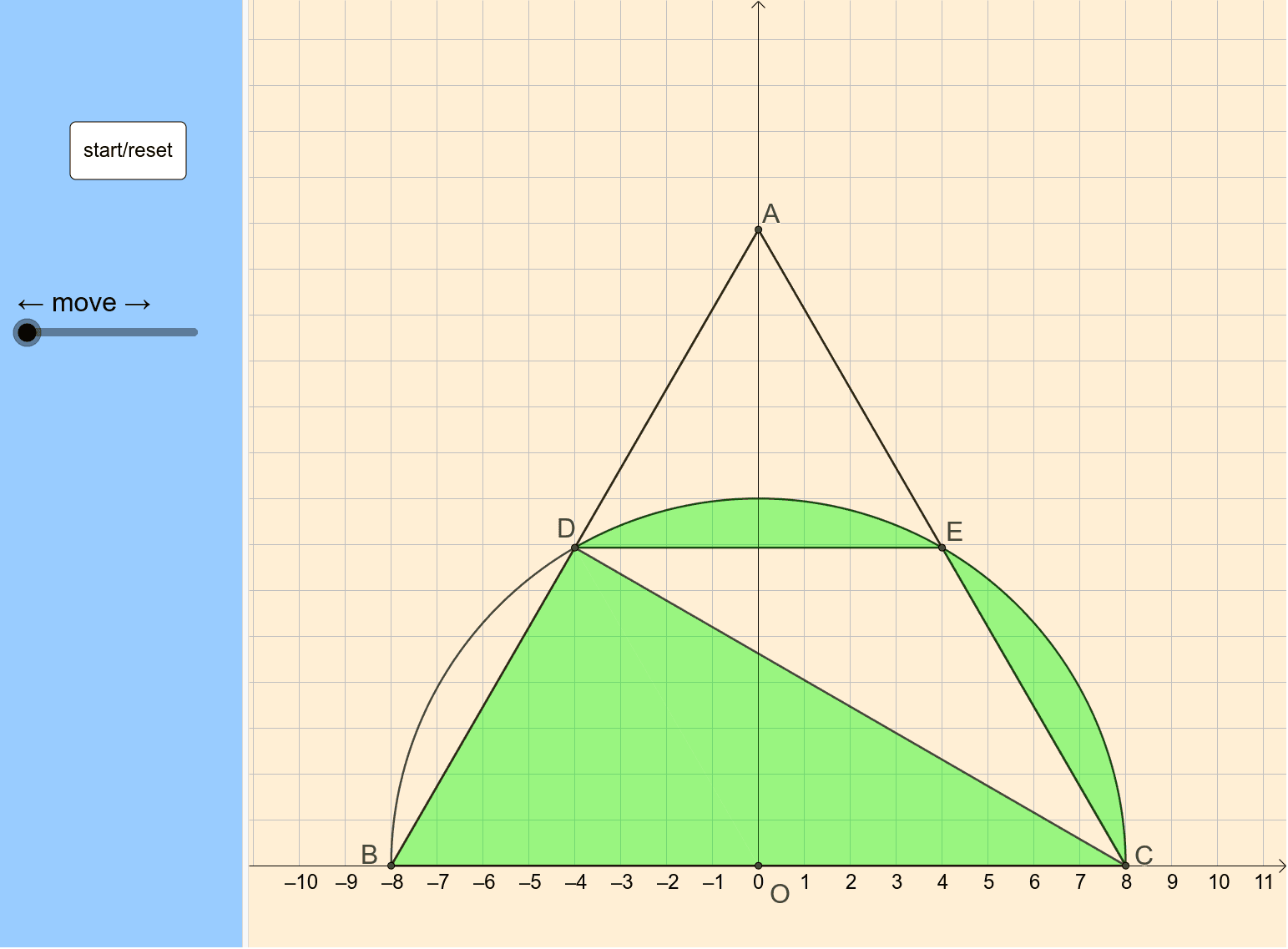



平面図形 円とおうぎ形の面積 Geogebra



正方形とおうぎ形 Weekly Sapixより どう解く 中学受験算数
円の面積=半径×半径×314であるから 円周=直径×314であるから 数学15章平面図形「円とおうぎ形」<準備問題②> 組 番 名前 次の問いに答えなさい。 (1)円形のピザを,おうぎ形に等しく切り分けます。家族が3人,6人,8人のとき,それぞ れ1人分の中心角の大きさを求めなさい。 3人の円とおうぎ形 周の長さと面積 名前 影をつけた部分の面積を求めなさい。 1. (正方形と円の組み合わせ) (正方形と半円の組み合わせ) (正方形とおうぎ形の組み合わせ) (おうぎ形と半円の組み合わせ) 3 4 2 NO2 /4点 10cm 6cm 8cm 10cm 10cm40 360 =36π (cm2 ) 例題動画 半径と中心角から面積・弧を求める 例半径6cm, 弧の長さ5πcmのおうぎ形の中心角




おうぎ形に関する応用問題3選




円とおうぎ形 応用 無料で使える中学学習プリント
円(おうぎ形)の面積 のコピー 作成者 The Essential Math Meets, hase3desu 新しい教材 ツークッション;今回は 「おうぎ形の問題」 を学習しよう。 「おうぎ形」は覚えているよね? 円を分割 した、ピザのような形をした図形だね。 ここでは、おうぎ形の 「弧の長さ」 や 「面積」 、 「中心角」 などを求める問題をやっていくよ。18cm 18cm 18cm 30°




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




円 扇形 の面積 周や弧の長さの公式 数学fun
円の面積の活用では,半円やおうぎ形の面積について,それが円の一部である図形であるというイメー ジをもたせた上で,面積の求め方について友だちどうしで話し合わせるようにする。そのことにより,円 の面積の公式を活用することのよさに気付かせるとともに,その定着を図りたい。 (4大きい円の面積と、大きい円の中にある半円の面積4つ分の差は、 =㎠ よって、 答え ㎠ 面積④ 重なりや移動でできた面積 例題5 長方形と正方形が下の図のように重なっています。色の付いた部分の面積をおうぎ形OAB、OBDに着目してください。 どちらも中心角が90\(^circ\)のおうぎ形です。 点Oを中心におうぎ形OABを回転するとおうぎ形OBDとぴったりと重なります。 このように1つの円で 等しい中心角に対する弧の長さは等しく 、 という関係があります。
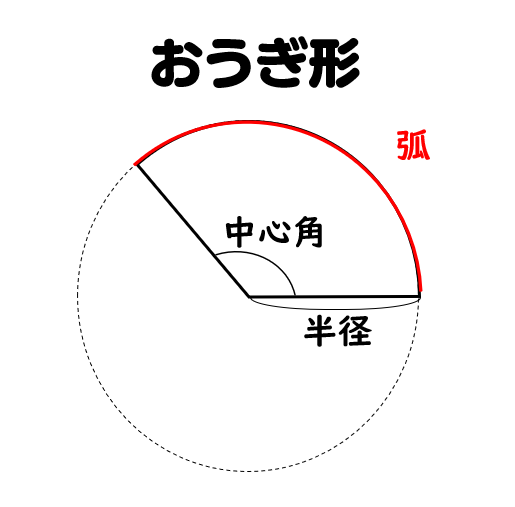



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun
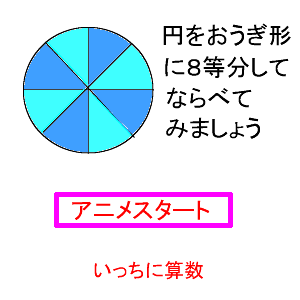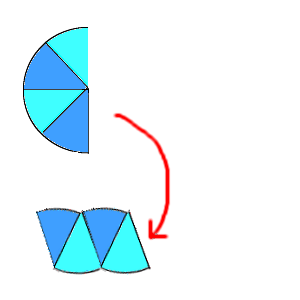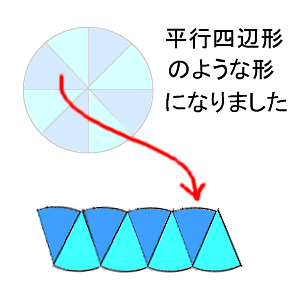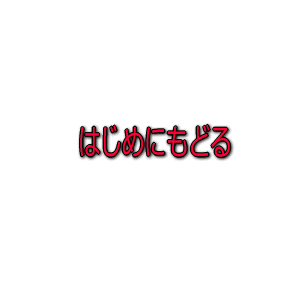



6年算数 円の面積 2 わかる教え方
中 心 角 360 °「おうぎ形の面積は、1/2×弧の長さ×半径」になる説明 まずはじめに、半径rの円の「面積」と「円周」の式を確認しておきます。 円の面積の式 $$\Large{π}r^2$$ 円の円周の式 $$\Large{2}{π}{r}$$円とおうぎ形⑺ 正三角形が関係する問題 10 10 次の図は、半径2㎝の円を7つ、それぞれの円の中心で交わるように 組み合わせた図形です。色のついた部分の面積を求めなさい。ただし円 周率は314と
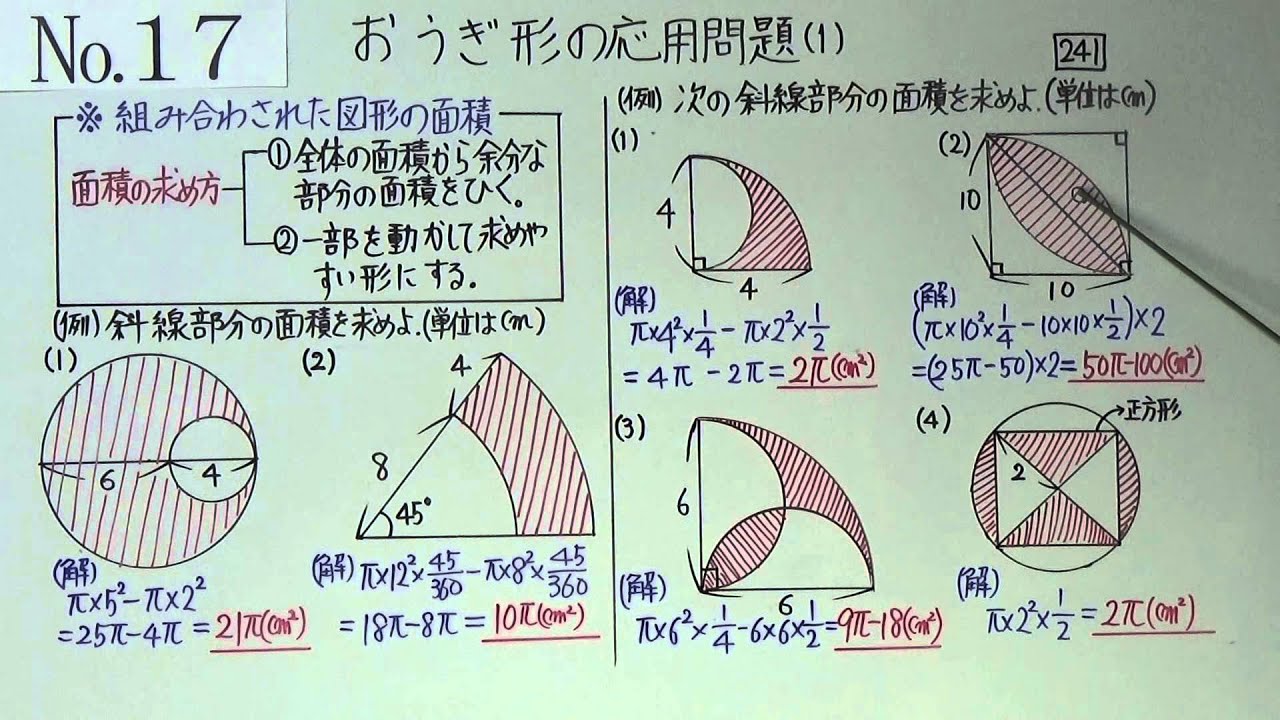



中1 17 2 おうぎ形の応用 1 Youtube



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典
円とおうぎ形の面積(唇の形) くちびるオバケとは? 正方形におうぎ形を組み合わせた問題は定番です。 こういうものを僕は『くちびるオバケ』などと呼んでいます。そういった名前をつけると子供が覚えやすいんですよね。この赤い部分の面積をすぐに求めようというのが、この記事の中学受験の算数・理科ヘクトパスカルによる四谷大塚予習シリーズ算数「平面図形(円とおうぎ形の面積)の問題」の手書き解説です。右の図のように直径が重なった 2つの半円があ ります。小さい半円の中心はAで ,半径は 30cm, 大きい半円の中心はBで ,半径は40cmです。A 360 面積 S = πr2 ×
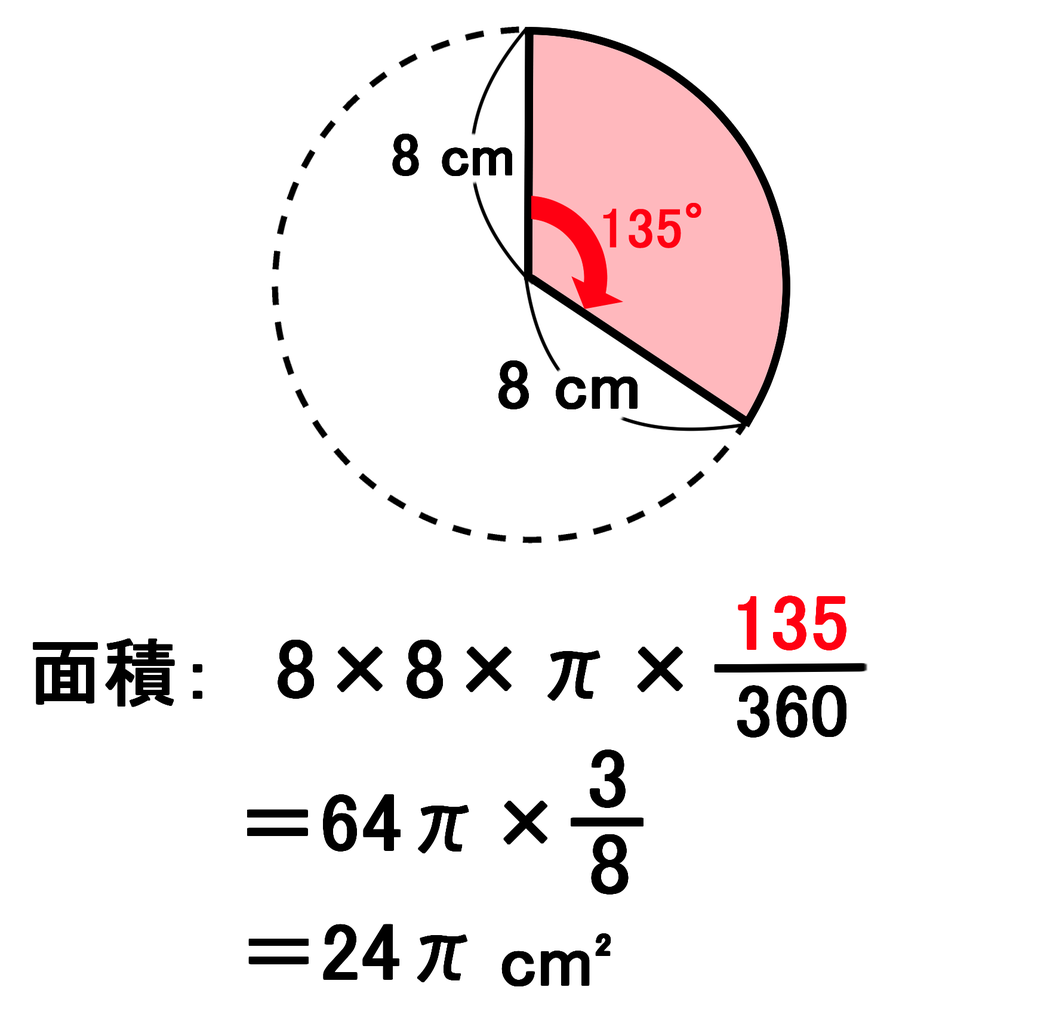



おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun
円の面積の公式を導き出そうとしている。 (算数への関心・意欲・態度) 円の面積の求め方を考えている。 (数学的な考え方) (2)展開 学習活動 おもな発問( ) 予想される児童の反応(C) 指導上の留意点(・) 評価( ) <研究との関わり> 時間 1 本時の問題をと らえる。 2 課題をまず円の面積を求めます。円の面積 $C$ は(2)式を用いて表せます。 $C = {\pi}r^{2}\tag{2}$ また求めるおうぎ形の中心角の大きさを $\alpha^{\circ}$ とすると求めるおうぎ形の面積 $S$ は(3)式で表せます。 $S = \frac{\alpha}{360} \times {\pi}r^{2}\tag{3}$α / 360 「円とおうぎ形」がテストにでるときに確認したいね^^ おうぎ形の




Bar2 Descubre Como Resolverlo En Qanda



みんなの算数オンライン 中学受験 4年 円とおうぎ形 円と面積応用 トレーニング
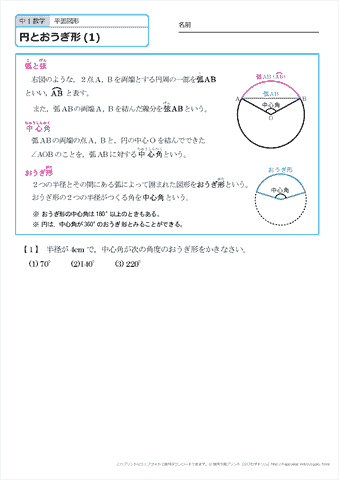
40 360 =4π (cm) 面積=324π×円やおうぎ形の中心が正しく把握できているかを確認してみてください。 「第32回 デイリーサポート 平面図形(1)」重要ポイントを含む問題(抜粋) A問題1 下図の斜線部分の面積は何cm 2 ですか。(ただし円周率は314とします。) このA問題を発展させた問題が、「15年度 開成中 大問2円とおうぎ形① 円周率を314 として、次の各問いに答えましょう。 1 右の図のような、半径4cm の円があります。 (1) この円の周りの長さは何cm ですか。 (2) この円の面積は何㎠ですか。 2 右の図のような、半径6cm の半円があります。
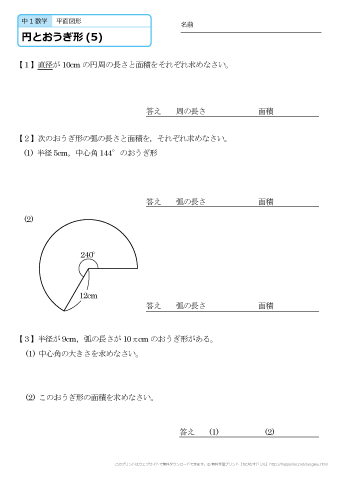



中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



円と扇形 中学受験ー算数解き方ポータル
Copy of 点の存在範囲(3Dボタン式残像ボタン) 松かさとアルキメデスらせん Pinecone



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Yaruki Suugaku Documents M1014 Pdf




円 おうぎ形 の面積 Geogebra
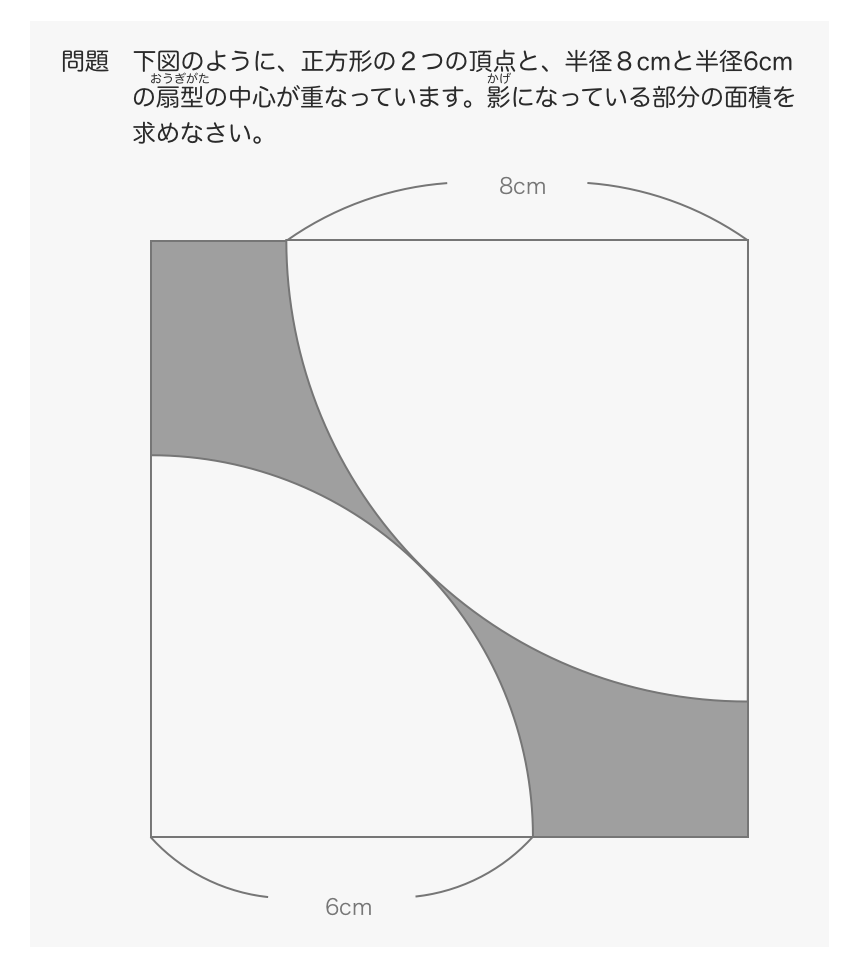



自作教材 円と扇形2 本質と技とコツ カテキョウブログ




中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
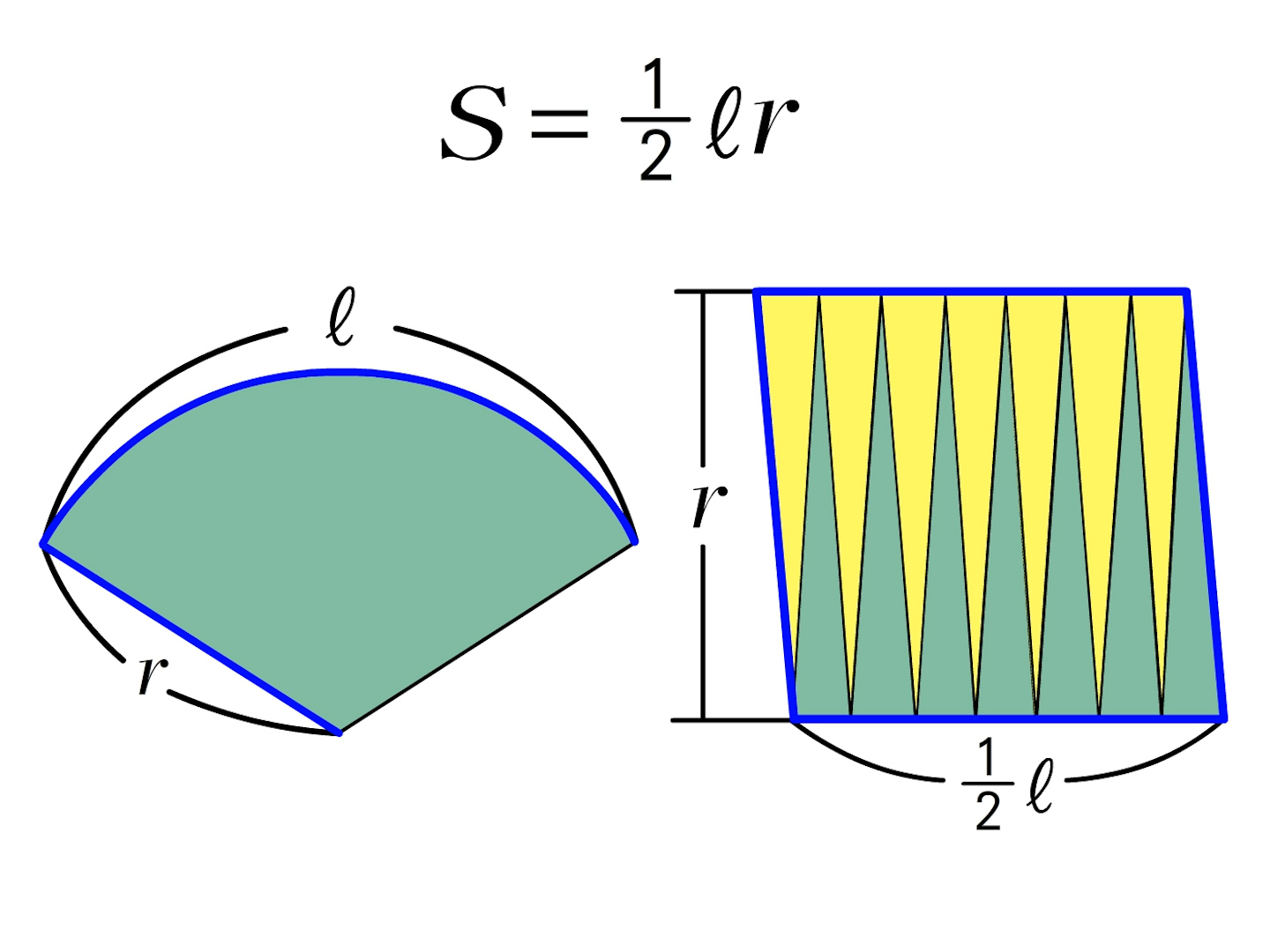



1年 おうぎ形の面積 数学イメージ動画集 大日本図書
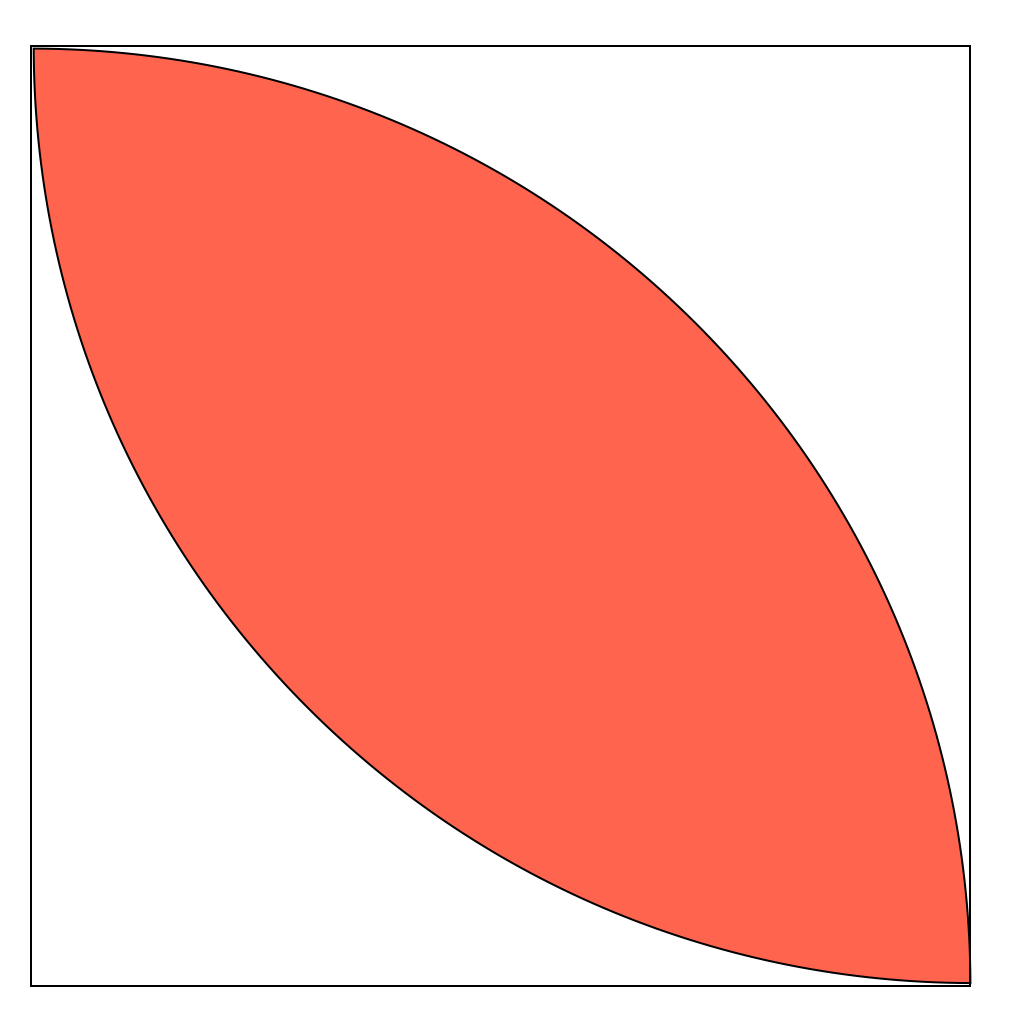



円とおうぎ形の面積 唇の形 カテキョウブログ




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学



Studydoctorおうぎ形の公式と忘れない考え方 中学1年数学 Studydoctor



Mathematics 平面図形 おうぎ形 働きアリ




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




応用 おうぎ形と正方形の面積 なかけんの数学ノート
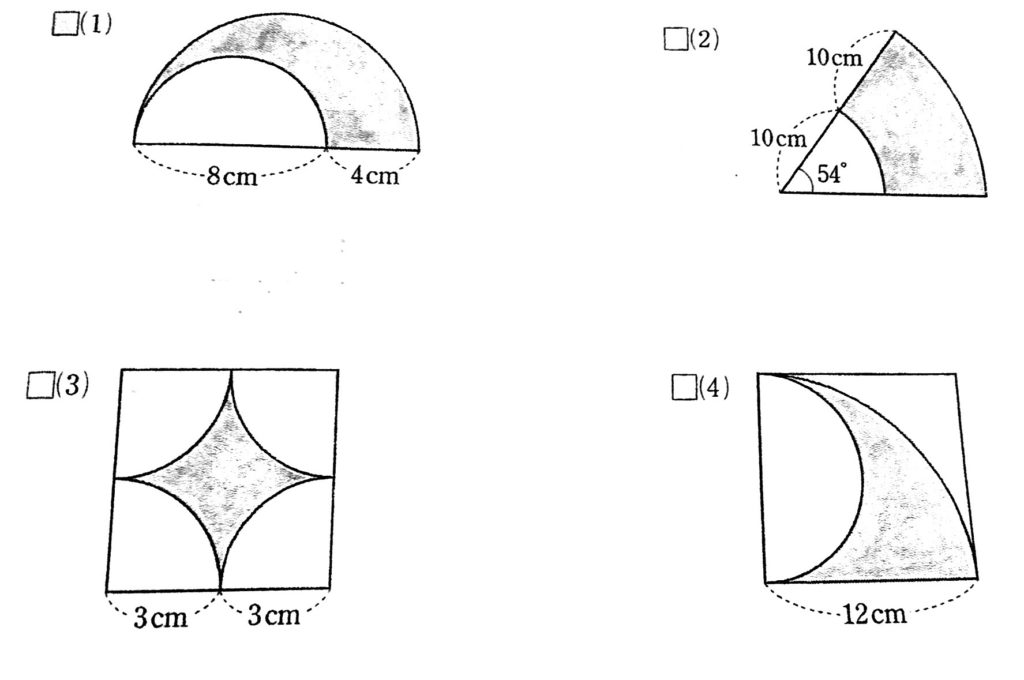



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ




おうぎ形 の弧の長さと面積 計算ドリル 問題集 数学fun



中1数学 円とおうぎ形 では 円の性質とおうぎ形の面積の求め方が項目理解の重要ポイント 桜華塾 お役立ちブログ 楽天ブログ




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト



円とおうぎ形 中学受験 田中貴 Com




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




円とおうぎ形 応用 無料で使える中学学習プリント




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり
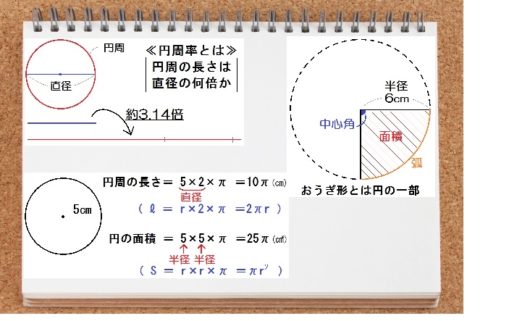



中学数学 平面図形 のコツ 円とおうぎ形




円とおうぎ形の特徴について 数学の要点まとめ 練習問題一覧



1




小学校6年生の算数 数学fun 数学 小学校 算数 算数




平面図形 おうぎ形の中心角 中学数学 定期テスト対策サイト
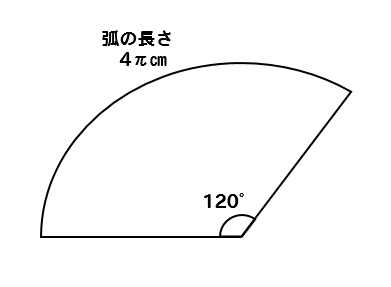



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook



3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



半円と扇形が重なってる部分の面積の求め方どうやったら良いですか 黒く塗 Yahoo 知恵袋



中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




標準 おうぎ形と正方形の面積 なかけんの数学ノート




Bar2right 8 Cm C0 I1 Descubre Como Resolverlo En Qanda




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



3



小5の学習ポイント2 円とおうぎ形 前田昌宏の中学受験が楽しくなる算数塾




なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル




中1数学のおうぎ形の公式が覚えられません そろそろテストなのでやばいんです 今はとに Clear




中学1年数学練習問題 円とおうぎ形の面積 円周 孤の長さ 空間図形




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学



Math 円の問題を解くときに使う3つの技 全体 白 分配法則 移動 働きアリ



無料 中1数学 基本問題 問題プリント 平面図形5 おうぎ形の弧と面積 138
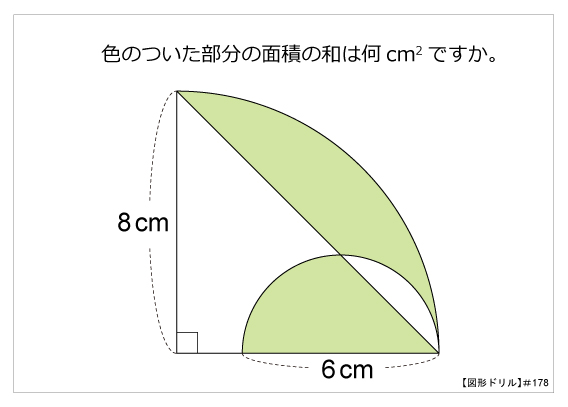



図形ドリル 第178問 おうぎ形の複合図形 算数星人のweb問題集 中学受験算数の問題に挑戦




おうぎ形の面積と弧の長さの公式 全国 中学数学ができるようになるブログ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学1年生 おうぎ型の弧の長さと面積 公式 個別進学教室マナラボ受験 教育情報サイト




扇形の面積の求め方 公式と計算例
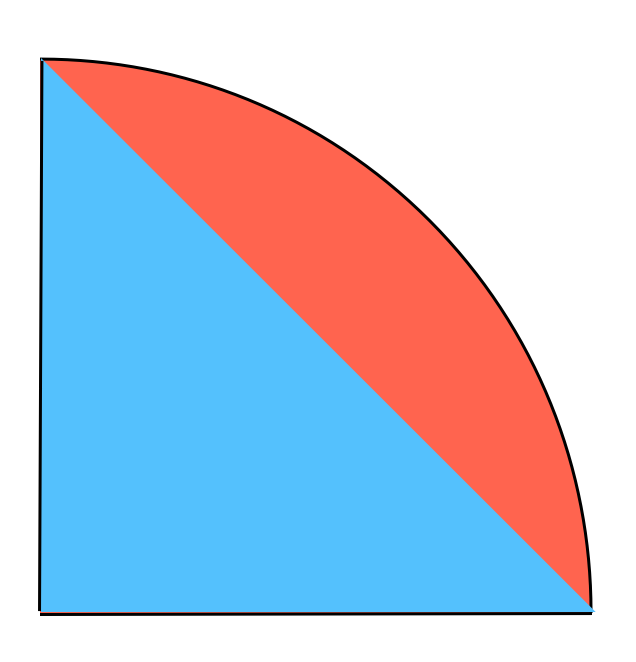



円とおうぎ形の面積 唇の形 カテキョウブログ
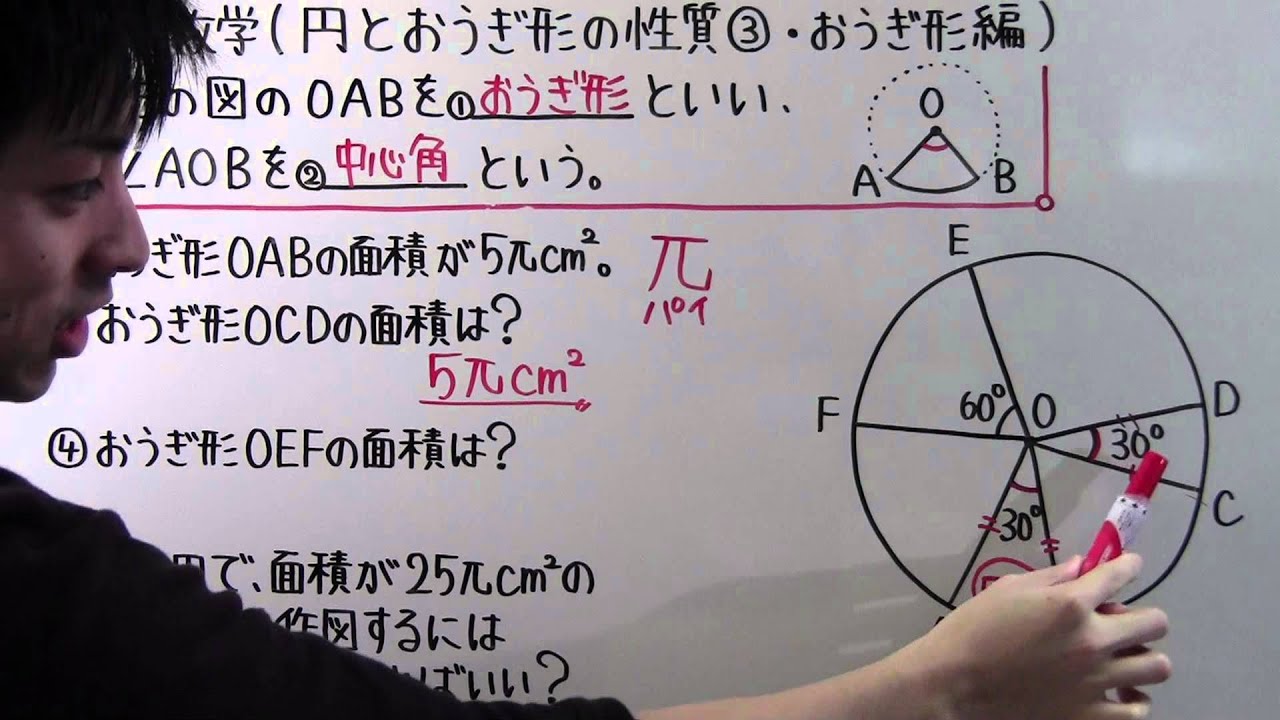



中1 数学 中1 74 円とおうぎ形の性質 おうぎ形編 Youtube
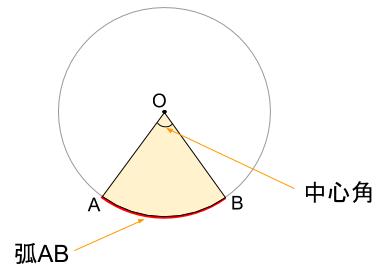



中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su




おうぎ形 色のついた面積の求め方 数学の記録




中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube



Math 平面図形 おうぎ形 働きアリ The 2nd




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




算数 本当に 分かる という事 おうぎ形の面積その1 エース学院




おうぎ形の問題 ちょっと応用編 切り取って求める 苦手な数学を簡単に




扇形の面積の求め方 公式と計算例
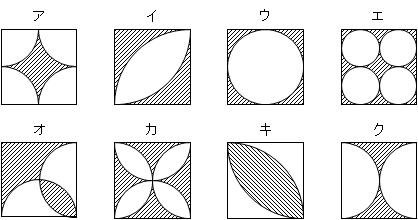



小5の学習ポイント2 円とおうぎ形 前田昌宏の中学受験が楽しくなる算数塾



1




中1 数学 中1 74 おうぎ形の弧と面積 Youtube
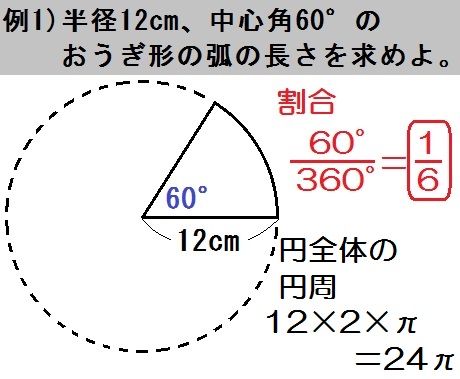



中学数学 平面図形 のコツ 円とおうぎ形




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




中学1年の数学 動画 円とおうぎ形の性 おうぎ形編の問題 19ch
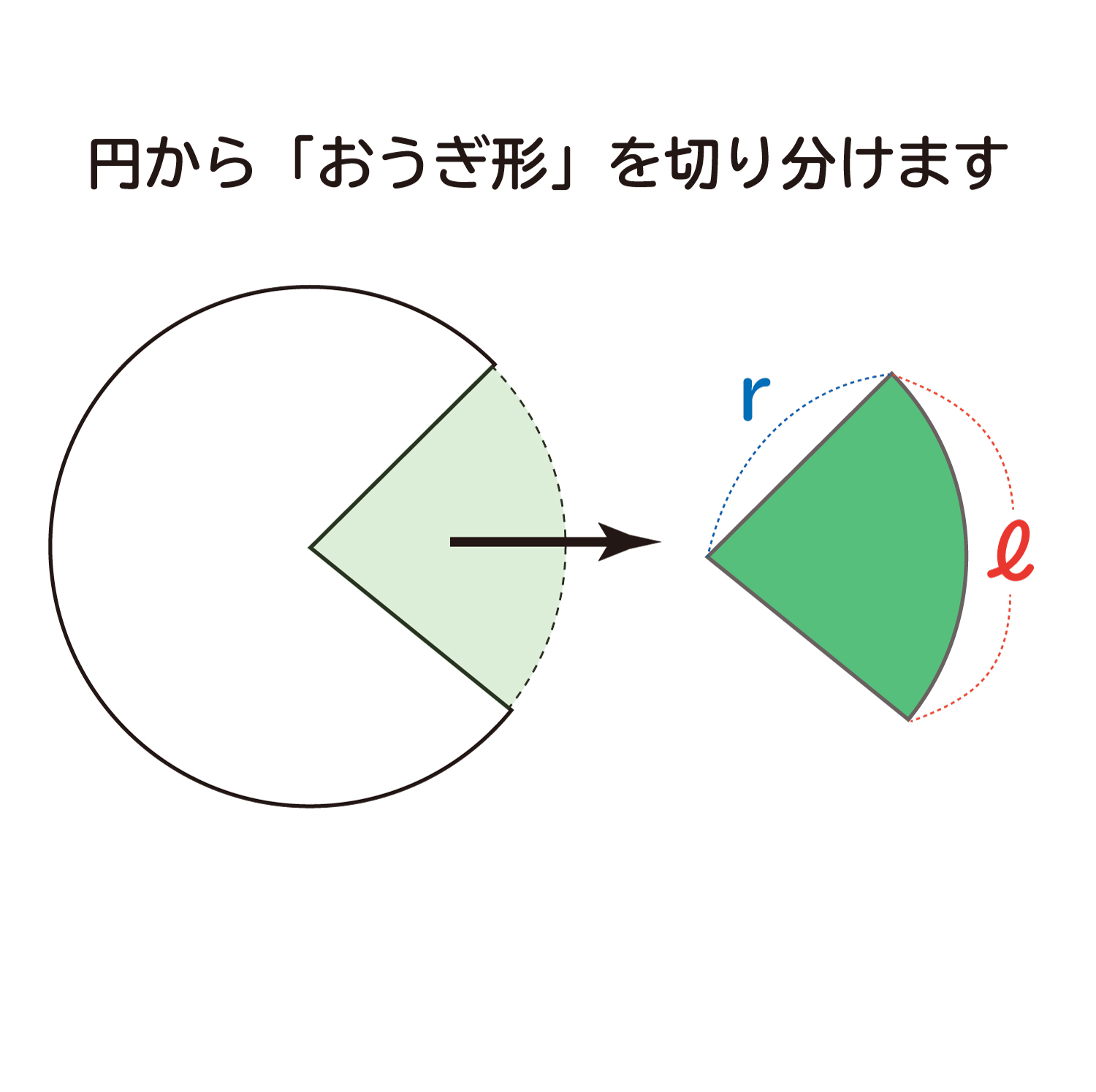



なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル




โน ตของ 中1 数学 おうぎ形 これで基礎バッチリ ช น Junior Clear
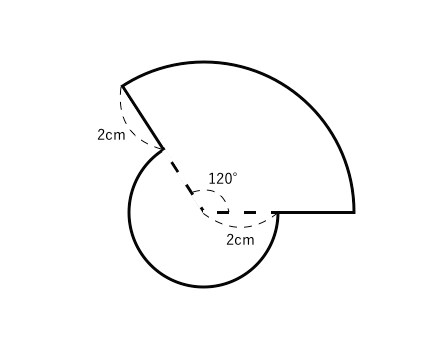



おうぎ形の問題 ちょっと応用編 苦手な数学を簡単に



5 第5章平面図形 円とおうぎ形 おうぎ形の面積 中学生




中学受験 算数 9月 円とおうぎ形 つるかめ算 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




おうぎ形の面積 弧度法との関連から眺める 身勝手な主張




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり




円 扇形 の面積 周や弧の長さの公式 数学fun



3



無料 中1数学 基本問題 解答プリント 平面図形5 おうぎ形の弧と面積 138




おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり
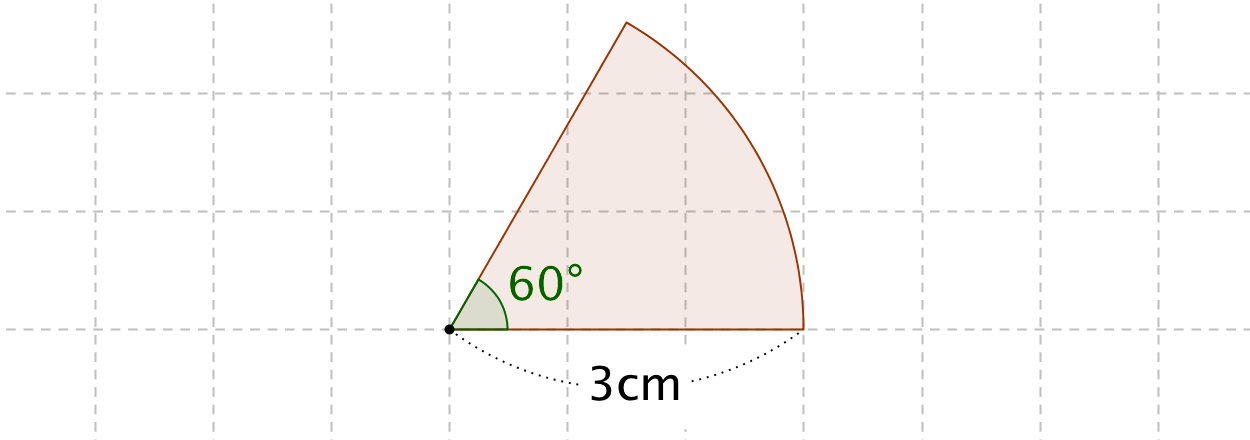



おうぎ形の面積の公式 算数の公式



問題93おうぎ形の面積




半円を回転させる面積の問題 プリントを使って自分で解こう



0 件のコメント:
コメントを投稿