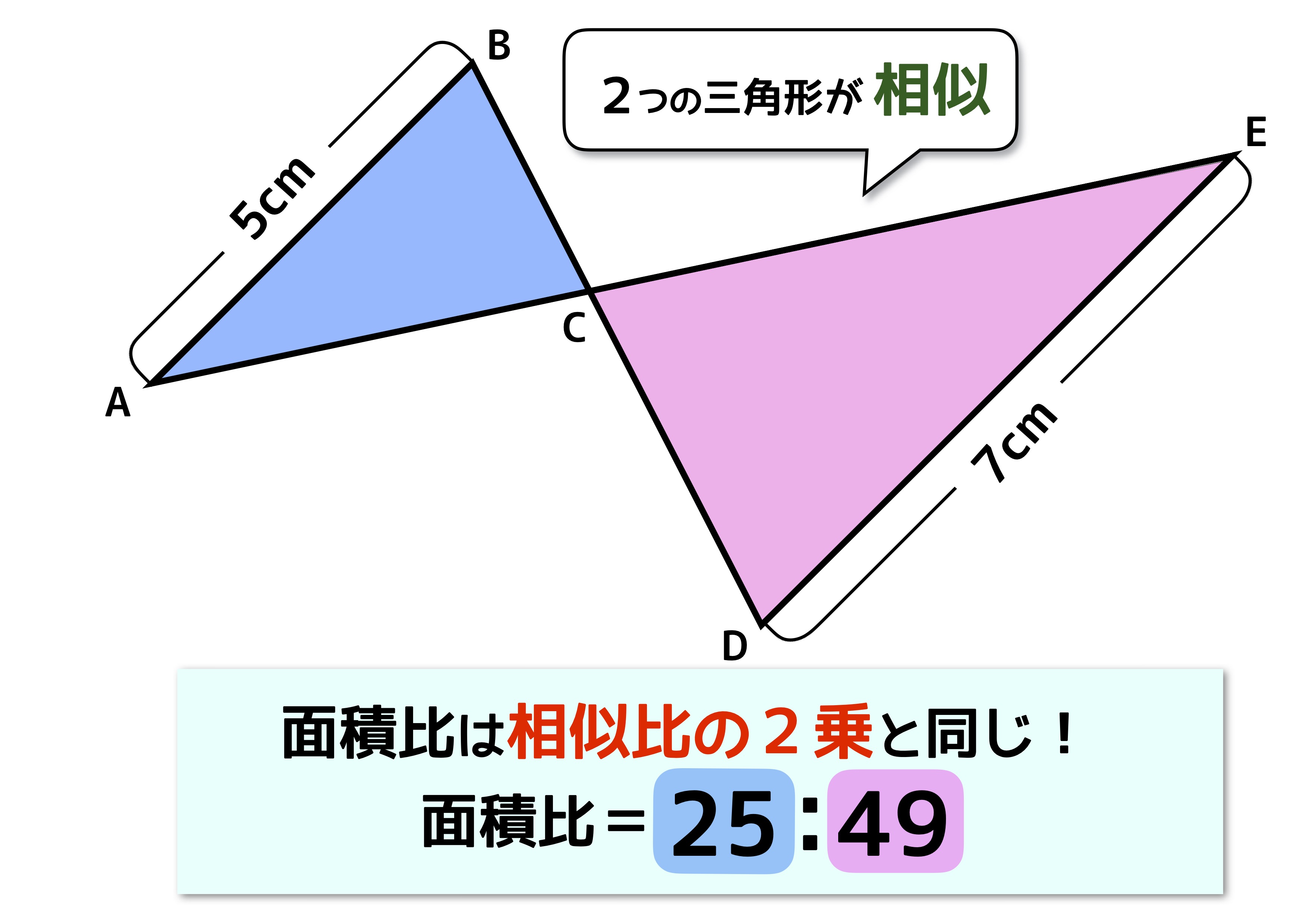
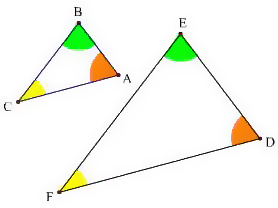
補角をなす三角形の面積比 解説 2つの角∠a,∠bが,∠a∠b=180°となるとき,∠aと∠bは,たがいに補角の関係にあるといいます。 ここで次の図のように,1組の角(∠bcaと∠ecd)がたがいに補角をなす(∠bca∠ecd=180°)三角形( abcと ecd)の面積比を考えます。海城中三角形の面積比 21年 21年 6年生 入試解説 東京 男子校 面積比 ★★★★☆☆(中学入試難関校レベル) 印象に残った入試問題の良問を「今年の1問」と題して取り上げています。 志望校への腕試しや,重要項目の確認に是非ご活用下さい。次の図の ABCと ADEのように,1つの角(∠A)が共有されている2つの三角形の面積比について考えます。 ABC ABE=CAEA=bd(=abad)① ABE ADE=ABAD=ac(=adcd)② となり,1つの角を共有する2つの三角形の面積比は,その共有する角をはさむ2辺の積の比と等しくなります。
相似三角形面积比和边长比的关系 高三网
三角形 相似 面積比
三角形 相似 面積比- その三角形と全体の図形の 面積比(「全体の図形の何倍か?」)を 求める問題を解くコツについて まとめます。 1.「高さが同じ三角形の面積比は 底辺の長さの比と同じになる」 という考え方を利用する。 2.三角形が複雑な図形の中に 面積比は高さの等しい三角形の組を探す!相似は2乗!① ダイヤグラムは速さのグラフ!相似・比率・逆比で読み解く 平行線+三角形の相似 辺の比と相似のテクニック2つ! 辺の比と連比はテクニック2つ!(共通の辺を2つの比で→最小公倍数で揃える) 直角三角形の相似(「3:4:5」




中考数复习二部分空间与图形十九课时相似三角形练习下载 Word模板 爱问共享资料
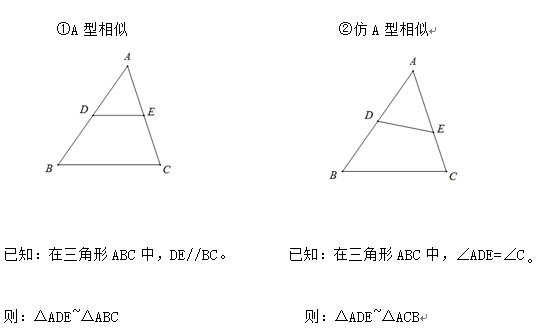
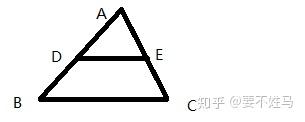
2つの三角形が相似の関係や 頂点が同一で高さが同じ三角形であれば 直接面積を比べることができますが、 そうでない場合は どのようにすればよいのでしょうか? このように 直接2つの図形を比べることができない場合は、 2つの三角形それぞれからみて 基準にできる共通な図形 を探して相似 相似と面積比 相似な三角形の対応する辺の比は等しいので adab=aeac=debc ② f eを通りabと平行な直線をひき、bcとの交点をfとする。 adeと efcにおいて de//bcより平行線の同位角は等しいので∠aed=∠ecf ab//efより平行線の同位角は等しいので∠ead=∠cef よって2組の角がそれぞれ等しい相似形の面積比の基本 相似形であるとわかる条件が提示されている問題では、相似になっている三角形の3つの辺のうち、どこか1つでも比がわかれば面積比が計算できます。 相似比は底辺の比であり、高さの比でもあるため、 面積比は相似比の二乗 で求められます。
まず abe、 abc共に縦は同じです。 補足 aから下に垂直な線が縦になります。 なので面積の違いは横の長さです beは12 bcは12 4 = 16 です。 abcと abeの面積比は 16 12 = 4 3 になります。 次に abeとabdの面積比を求めましす。 これも縦は共に同じです。 高さが共通の隣り合う三角形の面積比は底辺比に等しい。 これが最重要の型のひとつです。 相似な関係にある2つの平面図形の相似比がa:bの場合、面積比はa 2 :b 2 になる という性質が思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 図形ドリル 台形を対角線で区切って4つの部分に分けました。アはイよりも9 cm2,ウはエよりも12 cm2小さいとき,アとエの面積比は何対何
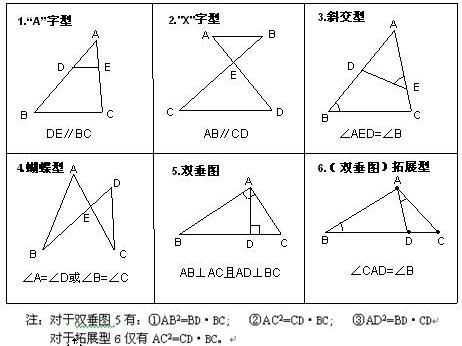
一行目に「⊿ adp ∽⊿ ebp だから」とあるけれど、まず解答でこの三角形の相似に着目したことがすんなりと理解できるだろうか? 説明できるか? 求めたい⊿はオレンジで囲った部分と緑で囲った部分だよ。しかも面積比を求めろと言っているのに、ここから⊿ adp ∽⊿ ebp の相似に注目しよう三角形の相似条件 問題3 正解3 解説3 問題4 正解4 解説4 相似の証明:2辺の比とその間の角 問題5 正解5 解説5 ----- 相似の証明:2組の角が等しい 問題6 正解6 解説6 ----- 相似の証明:直角三角形相似な図形と線分比と平行の関係、その計算方法と図形をとらえる視点について応用問題を含めて学習します。 三角形と線分比 平行線と線分比 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似




中考数学 在平行四边形中 怎么求3个三角形面积的比值 每日头条



对应角 信息图文欣赏 信息村 K0w0m Com
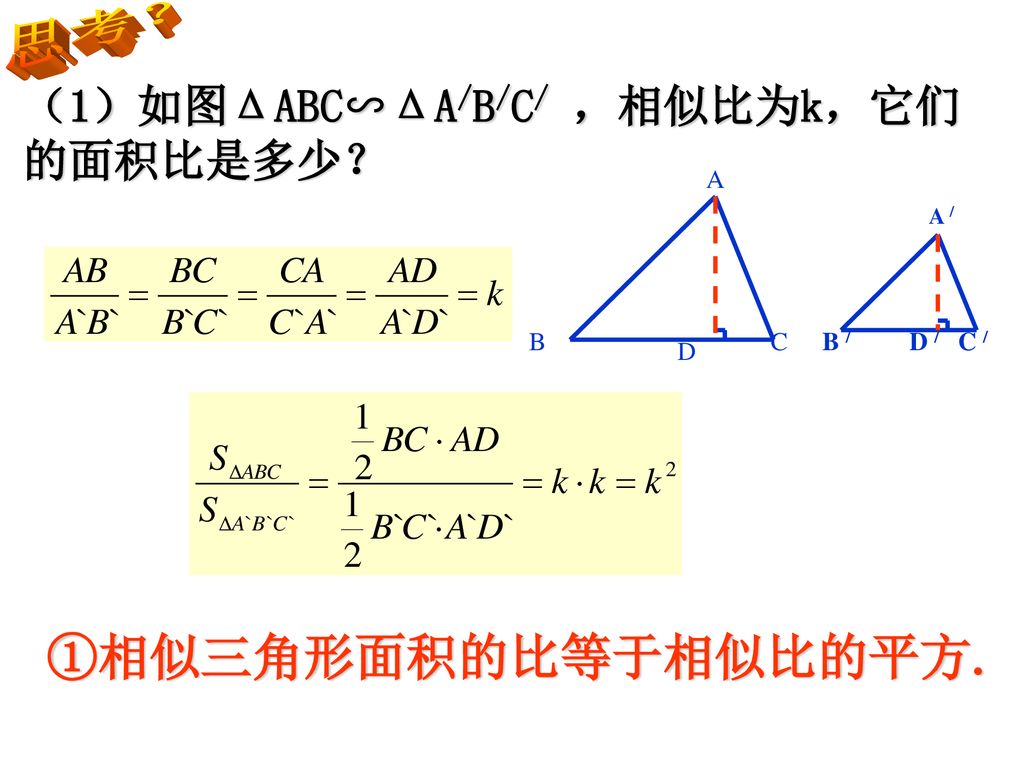
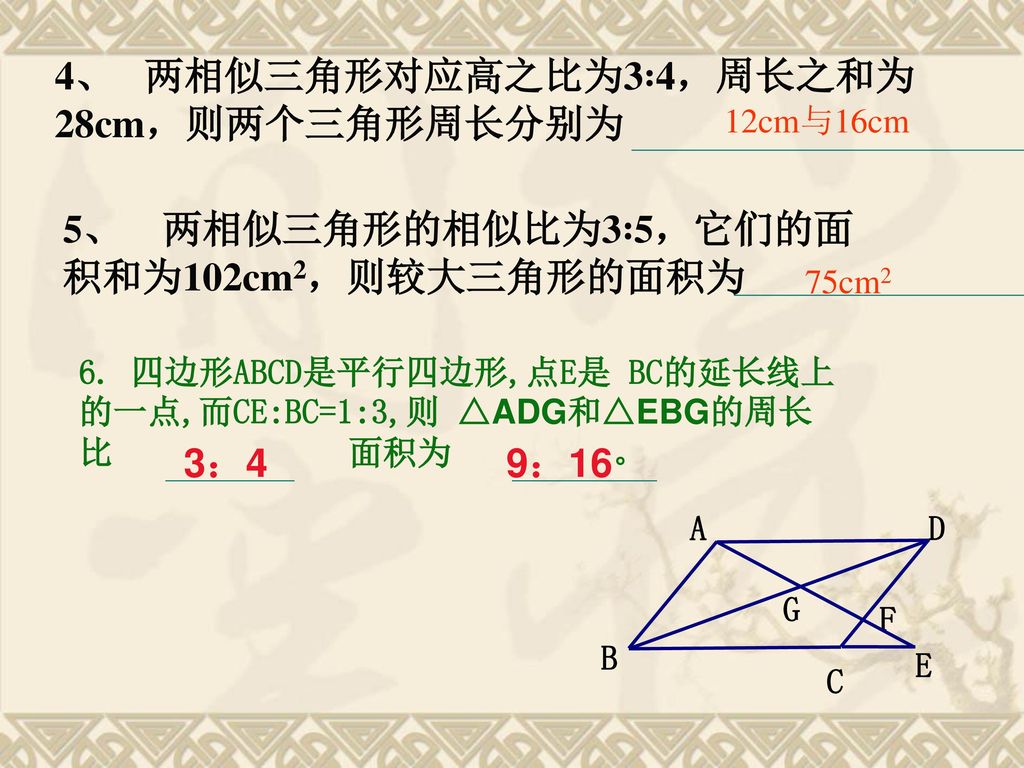
5章 相似な図形 底辺の比と面積比 右の図の ¼abc で,ad:db=2:3,ae:ec=5:4 のと き,次の三角形の面積比を求めなさい。 ⑴ ¼abe:¼abc 〔〕 ⑵ ¼dbe:¼abc 〔〕 相似な図形の面積比① 次の問に答えなさい。 また小さい三角形の面積が 75cm2 75 c m 2 のとき大きな三角形の面積は何 cm2 c m 2 ですか。 相似比が 5 9 5 9 なので、面積比はこの比の2乗なので 2581 25 81 となります。 次に大きな三角形の面積を求めます。 面積比が 2581 25 81 ということが分かっているので、 75× 81 25 =243 75 × 81 25 = 243 となるので、大きいほうの三角形の面積は243ということになります。 相似 上の図において、 ABCと A'B'C'の相似比が1:2であるとしましょう。 このとき、 ABCと A'B'C'の面積比はどうなるでしょうか。 先ほど確認したとおり、三角形の面積は「(底辺)×(高さ)× 1 2 1 2 」です。 底辺の比は、相似比なので、1:2。 高さの比も相似比と同様に1:2ですね。 どちらの三角形の面積も 1 2 1 2 をかけるので、 ABC: A'B'C'=1×1:2×2



相似三角形的面积比 初三网



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
面積比の公式3選とは三角形 さて、今までの話を踏まえ、ここからは「 相似じゃない図形の面積比 」について考えていきます。 具体的には 高さが等しい三角形;例 相似な図形の例 直線, 正三角形, 直角二等辺三角形, 正方形, 正多角形, 円, 放物線, 直角双曲線, 正多面体, 球など これらはそれぞれ、一方を適当な率で拡大または縮小し、適当に平行移動、回転、鏡映を施すと他方に重なる。 このとき双方は形が同じであるが、大きさと向き(平面上では2つの三角錐が相似であるとき、相似比、表面積比、体積比を求めましょう 相似比 → 2:3 表面積比 → 2 2 :3 2 → 4:9



相似形 搜狗百科



第四章相似形 图片欣赏中心 急不急图文 Jpjww Com
相似な三角形の面積比 以下の2つの三角形は相似です。 2つの三角形は相似。相似比は2:3 底辺の比が2:3なら、それぞれの高さの比も2:3です。ということで 相似な三角形の面積の比は相似比をそれぞれ2回かけたもの「直角三角形をつくる → 相似比を用いて計算をする」 にあります。 補助線には上記の3パターンがありますが、 オススメは 「影の先端が地面などと接している点から水平に書く」 と覚えやすい、 「水平パターン」です。 水平パターンを利用した解き方 上図より①=75m → ②=15m x=15mこの2つの三角形は相似になっているので、相似比を2乗して面積比を考えましょう。 よって、\( ABC\)と\( ADE\)の面積比は \(94\) となります。 次に、\( ADE\)と台形\(DBCE\)の面積比を考えてみま



9 6 相似三角形 知乎



相似三角形测试题不会做 极客名师为你解惑
面積比=相似比の二乗 相似比が a b ab a b のとき,面積比は S a S b = a 2 b 2 S_aS_b=a^2b^2 S a S b = a 2 b 2 図形を k k k 倍に拡大すると面積は k 2 k^2 k 2 倍になる相似な図形なら面積比は2乗の比になります。 相似な図形でない場合 (三角形を例に) ①底辺が同じ長さ面積比=高さの比 ②高さが同じ長さ面積比=底辺の比 多分これらを混同して覚えちゃっているのでは? 文房具屋 1年以上前 なるほど⭐️ありがとう慣れるまでは、小さい三角形を横に書き写して、その図を見比べて解くことをお勧めします。 相似な \(2\) つの三角形で、同じ色の辺同士が対応する辺です。 対応する辺の比が相似比です。 下図では相似比が \(43\) になっています。 ※\(86=1075=6448=43\)



相似三角形的面积 腾讯视频




朱式幸福 國中數學難題解析 3題 相似與比例
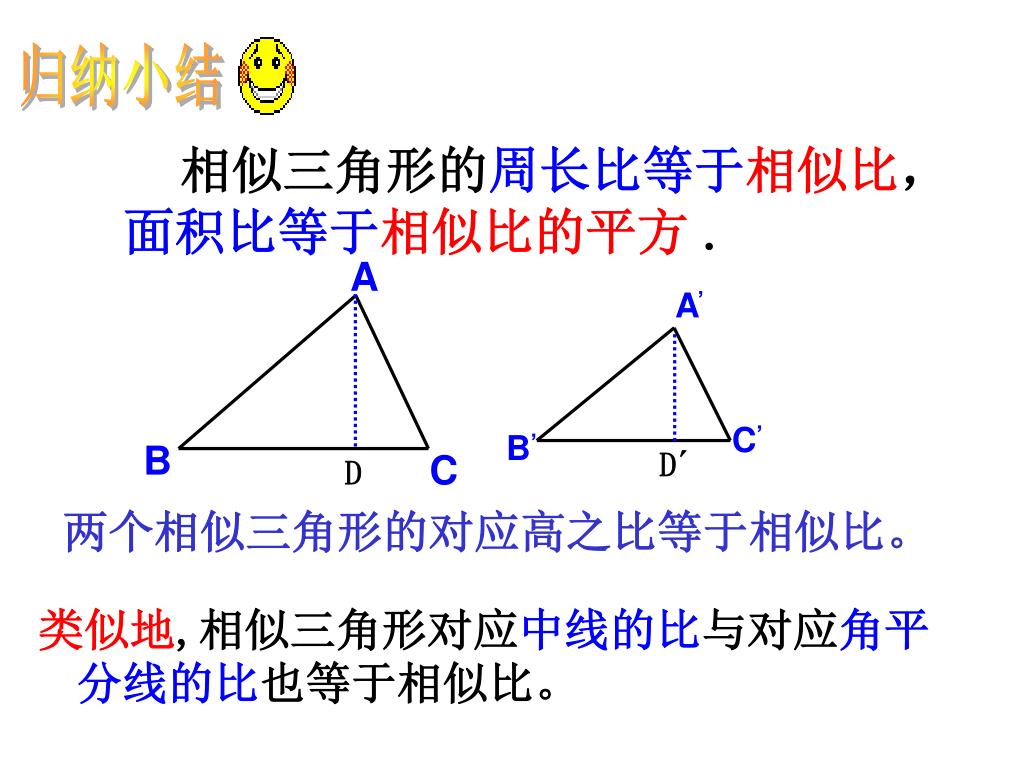
ここで、 adoと bcoが相似であることに再度注目してください。 adとbcの比率が2:3であるのなら、相似の関係であるため、do:boも\(2:3\)ということができます。 ①の型である adoと aboの底辺比が2:3なので、面積比も2:3。 ただし、先ほど求めた ado: bco=4:9という比の関係を維持しなくてはウ①相似比を用いて,相似な図形の 対応する辺の長さを求めることがで きる。(ノート) 3 2つの三角形が相似になるため の条件を調べる。 エ①三角形の相似条件の意味を理解 している。(小テスト) 4 ・ 5 三角形の相似条件を用いて,図形の 相似比から面積比を求める考え方はよく使うので、しっかり理解しておきましょう。 三角形の相似 ここからは、問題として最も多く使われる三角形の相似について詳しく見ていきましょう。 三角形の相似条件




等高三角形面積比 Youtube



1
数学・算数 多角形の面積比について 三角形の面積比は相似比の二乗となると思いますが、これは八角形など、どんな多角形にも応用できるのでしょうか? 質問No面積を求めていたものが突然相似比の性質を使って三角形の面積を求めさせられるから だ。 問 2つの三角形 P と Q は相似で、相似比は 2 : 3 である。P の面積が 4 のとき、Q の 面積はいくつか? この問題を解くには、次の基本的な公式が活躍する。 2つの図形 P と Q は相似で、相似比が m : n で 相似な図形の面積比は、 相似比の \(\bf{2}\) 乗 となります。 つまり、相似比が \(a b\) の図形では、面積比は \(\color{red}{a^2 b^2}\) となります。 三角形に限らず、どのような相似な図形においても、 面積比は相似比の \(\bf{2}\) 乗 となります。




相似の面積比を求める問題 上級編 Youtube




高校入試対策数学 面積比に関する対策問題 Pikuu
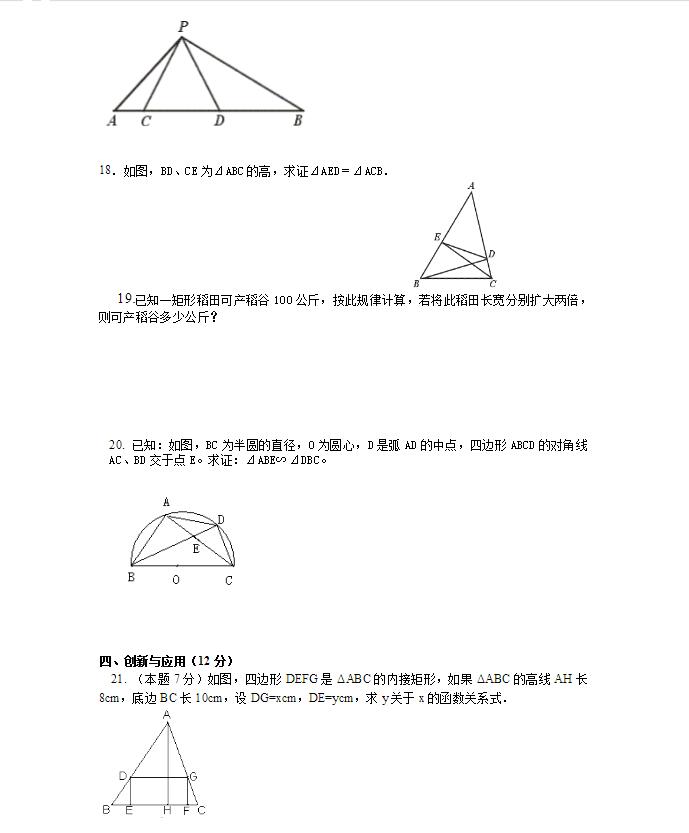
三角形abcと三角形adgは相似で、 辺の比は2:1。 よって、ef:dgは1:15=2:3。 三角形hefと三角形dhgは相似(2:3) なので、面積の比は4:9。 よって、三角形dhgの面積は135cm 2 。 dとe、gとfをそれぞれ結ぶ。 三角形dehと三角形ghfの面積はそれぞれ 9cm 2 。゚ 三角形の相似曵件。 ゜ 平行線および平行平面に関する線分の比についての性質。 ゞ 三角形および平行四辺形の性質。 (3) 縮図や立体図形の相似を通して,相似についての理解を济める。 ゚ 簡単な立体図形の相似,および相似形の相似比と面積比ン体相似な図形の面積比 相似な図形の面積の比は「相似比の \(2\) 乗の比」になります。 つまり、 相似比 \(ab\) の図形の面積の比は \(a^2b^2\) です。 なので 面積の比は \(a×ab×b\) となるわけです。 もちろん、三角形だけでなく、円や四角形や五角形やその他なんでも



相似三角形的性质 新授课 数学错题本 微信公众号文章阅读 Wemp




朱式幸福 國中數學 梯形對角線形成的三角形面積比
面積比と相似:図形の面積比は相似比の2乗 相似の図形の面積比は相似比の2乗 三角形が相似の場合、 面積比は相似比の2乗 と同じ相似比と面積比についての練習です。かなり基本的な話です。 苦手な人向けです。 次回追加分は面積について計算していくものになります。 17年9月12日 画像にあるような三角形の相似に関しての長さを求める問題です。 台形については、補助線がポイントです。難易度ちょい上がりますが三角形と比の性質や平行線と線分の比の性質は,三角形の相似条件を元に説明することができる。 図をかいたり,実測したり等の活動を通して性質に気付き,それを証明するという学習過程を重視 することによって,論理的思考力や直観力をのばすことができるよう心がけたい。 また,相似な



三角形的性质 万图壁纸网




觀念 相似三角形的周長比與面積比 Youtube



相似三角形的性质 相似ppt 第一ppt




Ppt 相似形與sss 相似性質powerpoint Presentation Free Download Id




相似三角形面积比



Q Tbn And9gct1cbhyzmpnguh0uf5t8bdkm4iqdb3jmof2blp0iaelv3tnivk8 Usqp Cau



相似三角形面积比和边长比的关系 高三网




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
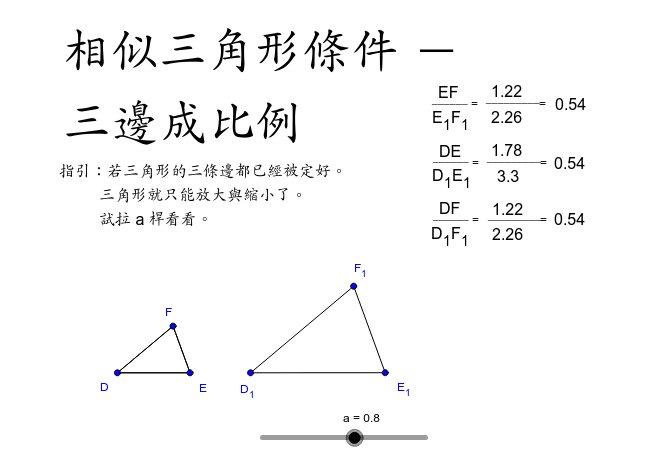



相似三角形條件 三邊成比例 Geogebra
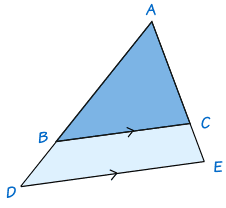



相似三角形定理



4 4相似三角形的性质极其应用一 Ppt 沃文网wodocx Com




高二物理自由落體 Clear
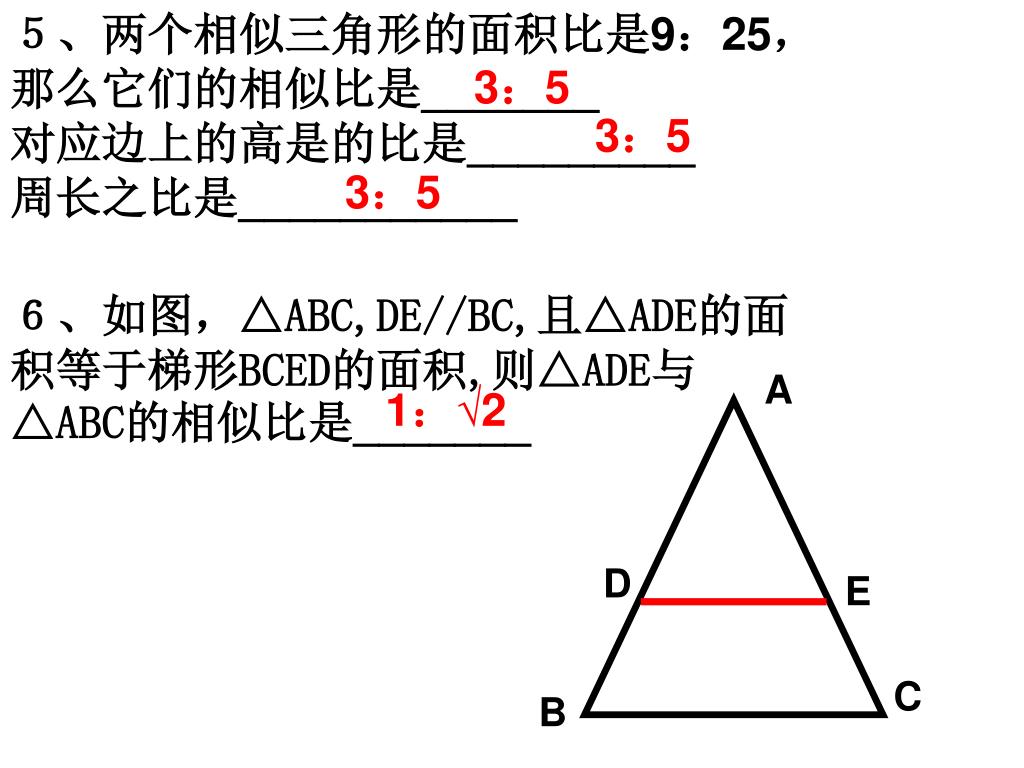



Ppt 27 2 3相似三角形的周长与面积powerpoint Presentation Id



什么叫比例中项 为什么相似三角形的面积比等于相似比的平方 尚书坊



相似三角形的面積比與邊長對應關係比 Live 多媒體數學觀念典online




李志鹏 古晋三中 分享我校数学教师林会颖老师的教学课件 指导初三学生学习相似三角形的面积比 古晋三中 线上教学




相似三角形的四个重要性质 对应角 对应边 周长比和面积比 九年级 下 数学 教学视频 哔哩哔哩 Bilibili




翻轉學習影片 國中 數學 試題解析 102試辦會考 選擇題第21題 相似三角形面積比與柱體的體積



打印预览




例題 相似三角形面積比 直角三角形 Youtube



这个数学核心考点 每年中考都会考 破解方法送给你
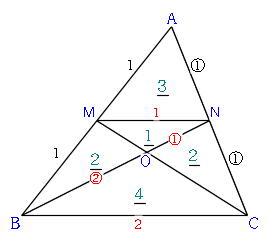



Mathematics 相似 4 面積と比 面積比は となりあった三角形で求める 働きアリ




相似三角形面积比例关系



相似三角形 维基百科 自由的百科全书



必杀 三角形37 相似三角形巧用相似面积比 第2届美国邀请赛题 哔哩哔哩 つロ干杯 Bilibili



数学 相似三角形系列03 面积比问题



前天刚考的公务员考试真题 3分钟 看看你能做对几道 三角形




三角度等于多少啊 一个三角形是多少度 三人行教育网 Www 3rxing Org




初中數學相似三角形的判定定理證明及利用三角形相似解決問題 每日頭條



相似三角形的问题 图片欣赏中心 急不急图文 Jpjww Com




基礎 相似三角形的周長比與面積比 數學 均一教育平台



比例线段 相似三角模型比例线段



数学 相似三角形系列03 面积比问题




第十章图形的相似 复习课 Ppt Download



1




相似三角形定理和性质



数学 相似三角形系列03 面积比问题



4 7 第2课时相似三角形的周长和面积之比 免费资源共享课件巴巴www Kejian Com公众号kejianbaba打包 Ppt 课件巴巴kejian Com 课件巴巴kejian Com




19 学年苏教版选修4 1 相似三角形的进一步认识课时作业 302edu教育资源网



27 2 3相似三角形的周长与面积 Ppt Download



数学 相似三角形系列03 面积比问题



腾讯视频



相似三角形的性质 图形的相似ppt 第2课时 第一ppt



北师大版初中数学九年级上册相似三角形的周长比与面积比公开课优质课课件教案视频 知乎




中考數學幾何知識重難點 相似三角形 每日頭條




Ppt 4 4 相似三角形的性质及其应用 1 Powerpoint Presentation Id




几何问题之相似三角形 网易订阅



学霸们 来看看这几道小升初后的入学分班数学压轴几何题 爱子网



218几何原本第六卷 命题19 相似三角形面积的比等于相似比的平方 哔哩哔哩 つロ干杯 Bilibili




相似三角形的面積比與邊長對應關係比 Live 多媒體數學觀念典online




面积比等于对应边的平方比 搜索结果 哔哩哔哩 Bilibili




周长 面积 比 在平面几何问题中的巧用 每日头条



初中数学知识点相似三角形的判定及性质




相似比と面積比 中学3年数学 Youtube




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




等高三角形的面積比 Live 多媒體數學觀念典online



Ppt 4 4 相似三角形的性质及其应用 1 Powerpoint Presentation Id



数学 相似三角形系列03 面积比问题



相似三角形边长比的关系 相似比与面积比的关系 相似三角形公式




相似比 從數學上來說 相似指兩個圖形的形狀完全相同 其中一個圖形能通過放 百科知識中文網



中考数学 轻松搞定相似三角形 考查



I03piccdn Sogoucdn Com 62fcd17a7



求不规则四边形的面积 给出的条件似乎没什么用 关键是求




4 7相似三角形的周长和面积之比 第2课时 课件 七七文库www 77wenku Com




數學清concept系列004 Ratios Of Areas Ample Edutainment Facebook




九年级数学下册相似三角形的周长与面积专题训练 题目较难 收藏 中考 四边形 网易订阅




小学阶段三角形问题五大模型 实题实练 每日头条



高中数学 相似三角形的性质 选修4 同桌100学习网




例題 相似三角形面積比的應用 數學 均一教育平台



Puui Qpic Cn Qqvideo Ori 0 248g8vl0r 496 280 0



第十章图形的相似 复习课 Ppt Download




相似三角形判定定理 1 平行於三角形一邊的直線和其他兩 華人百科



巧妙利用面积比等于相似比的平方比解题 哔哩哔哩 Bilibili




相似三角形的面積比 Isdp08am 隨意窩xuite日誌




中考数复习二部分空间与图形十九课时相似三角形练习下载 Word模板 爱问共享资料



高中数学 相似三角形的性质 选修4 同桌100学习网




几何原本 相似三角形面积比等于对应边的比 知识百科全书网站




相似三角形面積比與周長比 Youtube




中點三角形 維基百科 自由的百科全書



Amc 10 第三讲 运动的相似三角形 知乎




觀念 等高三角形面積比 Youtube



Priori Moe Gov Tw Download Textbook Math Grade9 Book5 Math 9 5 3 Pdf



1




九年级数学下册相似三角形的周长与面积专题训练 题目较难 收藏 中考 四边形 网易订阅




面积比等于对应边的平方比 搜索结果 哔哩哔哩 Bilibili



初中数学中求面积综合题让人毫无头绪 辅助线添加恰当则事半功倍
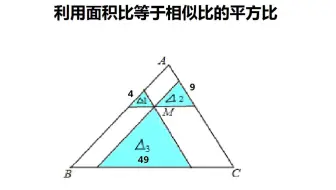



相以三角形面积的比等于相似比的平方解决实际问题 哔哩哔哩 Bilibili
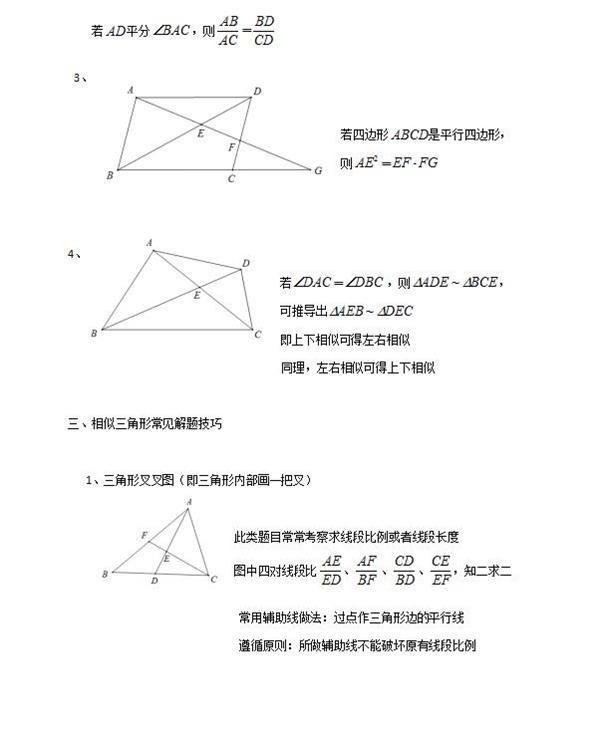



相似三角形测试题不会做 极客名师为你解惑



0 件のコメント:
コメントを投稿